GATE 2018
Question 1 |
“From where are they bringing their books? __________ bringing __________ books from __________.”
The words that best fill the blanks in the above sentence are
Their, they’re, there | |
They’re, their, there | |
There, their, they’re | |
They’re, there, there |
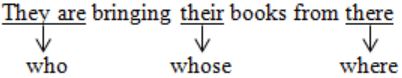
Question 2 |
"A _______ investigation can sometimes yield new facts, but typically organized ones are more successful."
The word that best fills the blank in the above sentence is
meandering | |
timely | |
consistent | |
systematic |
Question 3 |
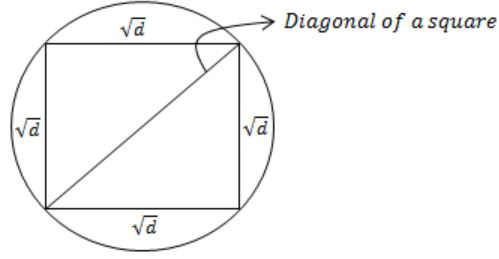
The area of a square is d. What is the area of the circle which has the diagonal of the square as its diameter?
πd | |
πd2 | |
(1/2)πd2 | |
(1/2)πd |
Area of a square A = a2 (where a is side)
In the question,
Area of a square = d
The side of a square = √d
Diagonal of a square = Diameter of circle
From Pythagoras theorem,
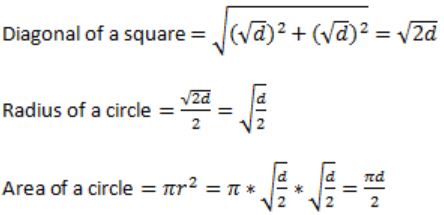
Question 4 |
What is the missing number in the following sequence?
2, 12, 60, 240, 720, 1440, _______, 02880 | |
1440 | |
720 | |
0 |
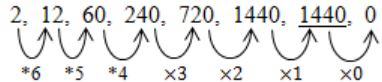
2 × 6 = 12
12 × 5 = 60
60 × 4 = 240
240 × 3 = 720
720 × 2 = 1440
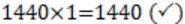
1440 × 0 = 0
Question 5 |
What would be the smallest natural number which when divided either by 20 or by 42 or by 76 leaves a remainder of '7' in each case?
3047 | |
6047 | |
7987 | |
63847 |
Take the LCM of 20, 42, 76 i.e., 7980.
⟹ Remainder = 7
⟹ Smallest number divisible by 20 (or) 42 (or) 72 which leaves remainder 7 is = 7980 + 7 = 7987
Method-II:
Option I:
3047 – 7 = 3040
3040 not divisible by 42
Option II:
6040 not divisible by 42
Option III:
7980 divisible by 20, 42, 76
Option IV:
63840 divisible by 20, 42, 76
→ Smallest (7980, 63840) = 7980
→ 7980 + remainder 7 = 7987
Question 6 |
If pqr ≠ 0 and p -x = 1/q, q -y = 1/r, r -z = 1/p, what is the value of the product xyz?
-1 | |
1/pqr | |
1 | |
pqr |
→ p-x = 1/q ⟹ 1/px = 1/q
⟹ q = px
⟹ log q = log px
⟹ x log p = log q
⟹ x = log q/ log p
→ q-y = 1/r ⟹ 1/qy = 1/r
⟹ qy = r
⟹ y log q = log r
⟹ y = log r/ log q
→ r-z = 1/p ⟹ 1/rz = 1/p
⟹ p = rz
⟹ log rz = log p
⟹ z log r = log p
⟹ z = log p/ log r
XYZ = log q/ log p * log r/ log q * log p/ log r =1
Question 7 |
In the figure below, ∠DEC + ∠BFC is equal to

∠BCD - ∠BAD | |
∠BAD + ∠BCF
| |
∠BAD + ∠BCD | |
∠CBA + ADC |
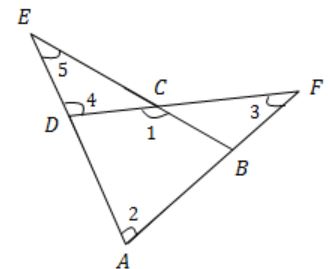
→ ∠1 = ∠5 + ∠4 ………(i)
According to triangular property:
Angle of exterior = sum of interior angles
→ ∠4 = ∠3 + ∠2 ……….(ii)
By substituting (ii) in (i)
→ ∠1 = ∠5 + ∠3 + ∠2
→ ∠1 = ∠BCD
∠2 = ∠BAD
→ ∠BCD - ∠BAD = ∠1 - ∠2
= ∠5 + ∠3 + ∠2 - ∠2
= ∠ 5 + ∠3
= ∠DEC + ∠BFC
Question 8 |
In a party, 60% of the invited guests are male and 40% are female. If 80% of the invited guests attended the party and if all the invited female guests attended, what would be the ratio of males to females among the attendees in the party?
2:3 | |
1:1 | |
3:2 | |
2:1 |
→ 60% invited guests are males i.e., 60 males
→ 40% invited guests are females i.e., 40 females
→ 80% invited guests are attended i.e., total guests attended to a party = 80
→ All the invited females are attended then remaining people are males = 80 – 40 = 40 males
⇒ 40 males : 40 females
⇒ 1 : 1
Question 9 |
In appreciation of the social improvements completed in a town, a wealthy philanthropist decided to gift Rs 750 to each male senior citizen in the town and Rs 1000 to each female senior citizen. Altogether, there were 300 senior citizens eligible for this gift. However, only 8/9th of the eligible men and 2/3rd of the eligible women claimed the gift. How much money (in Rupees) did the philanthropist give away in total?
1,50,000 | |
2,00,000 | |
1,75,000 | |
1,51,000 |
Female senior citizen’s gift = Rs. 1000
No. of males = a say
No. of females = b say
Altogether no. of persons eligible for gift = 300
i.e., a+b = 300
Total amount be given = (8x/9 × 750) + (2y/3 × 1000)
= (2000x/3) + (2000y/3)
= 2000/3 (x+y)
= 2000/3 (300)
= 2,00,000
Question 10 |
A six sided unbiased die with four green faces and two red faces is rolled seven times. Which of the following combinations is the most likely outcome of the experiment?
Three green faces and four red faces. | |
Four green faces and three red faces. | |
Five green faces and two red faces. | |
Six green faces and one red face. |
→ If we roll a die for six time then we get 4 green faces and 2 red faces.
→ And if we roll for seventh time green face can have more probability to become a outcome.
→ Then most likely outcome is five green faces and two red faces.
Question 11 |
The largest eigenvalue of A is ________
3 | |
4 | |
5 | |
6 |
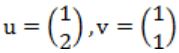
→ Correction in Explanation:
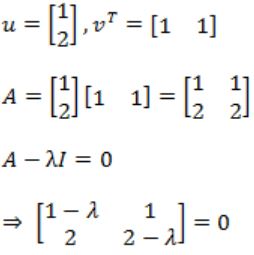
⇒ (1 - λ)(2 - λ) - 2 = 0
⇒ λ2 - 3λ=0
λ = 0, 3
So maximum is 3.
Question 12 |
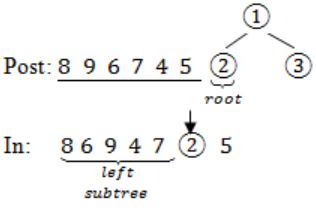
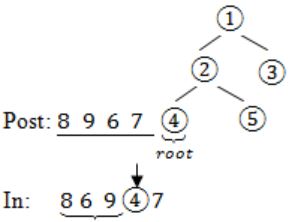
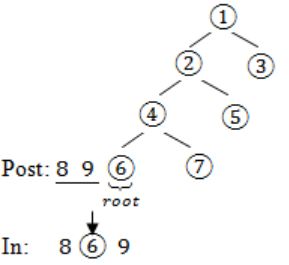
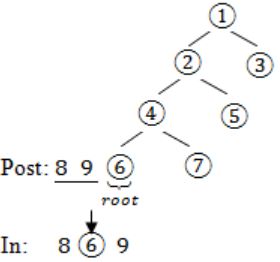
The postorder traversal of a binary tree is 8, 9, 6, 7, 4, 5, 2, 3, 1. The inorder traversal of the same tree is 8, 6, 9, 4, 7, 2, 5, 1, 3. The height of a tree is the length of the longest path from the root to any leaf. The height of the binary tree above is _______.
1 | |
2 | |
3 | |
4 |
In – 8 6 9 4 7 2 5 1 3
Post: 8 9 6 7 4 5 2 3 1→(root)
In: 8 6 9 4 7 2 5→(left subtree) 13→(right subtree)
Question 13 |
Two people, P and Q, decide to independently roll two identical dice, each with 6 faces, numbered 1 to 6. The person with the lower number wins. In case of a tie, they roll the dice repeatedly until there is no tie. Define a trial as a throw of the dice by P and Q. Assume that all 6 numbers on each dice are equi-probable and that all trials are independent. The probability (rounded to 3 decimal places) that one of them wins on the third trial is __________.
0.021 | |
0.022 | |
0.023 | |
0.024 |
⇾ A person wins who gets lower number compared to other person.
⇾ There could be “tie”, if they get same number.
Favorable cases = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
Probability (tie) = 6/36 (when two dice are thrown, sample space = 6 × 6 = 36)
= 1/6
“Find the probability that one of them wins in the third attempt"
⇾ Which means, first & second time it should be tie and third time it should not be tie
⇾ P (tie) * P (tie) * P (not tie)
⇒ 1/6* 1/6 * (1 - 1/6)
⇒ (5/36×6)
= 0.138/6
= 0.023
Question 14 |
In an Entity-Relationship (ER) model, suppose R is a many-to-one relationship from entity set E1 to entity set E2. Assume that E1 and E2 participate totally in R and that the cardinality of E1 is greater than the cardinality of E2.
Which one of the following is true about R?
Every entity in E1 is associated with exactly one entity in E2. | |
Some entity in E1 is associated with more than one entity in E2. | |
Every entity in E2 is associated with exactly one entity in E1. | |
Every entity in E2 is associated with at most one entity in E1.
|

The M : 1 relationship holds between two entities E1 and E2, in which each tuple from E2 is in relation with many tuples of E1. One tuple from E1 is in relation with only one tuple of E2. It is given that participation from both the sides is total and the cardinality of E1 is greater than E2.

Therefore, every entity E1 is associated with exactly one entity in E2.
Question 15 |
Consider a process executing on an operating system that uses demand paging. The average time for a memory access in the system is M units if the corresponding memory page is available in memory and D units if the memory access causes a page fault. It has been experimentally measured that the average time taken for a memory access in the process is X units.
Which one of the following is the correct expression for the page fault rate experienced by the process?
(D-M)/(X-M) | |
(X-M)/(D-M) | |
(D-X)/(D-M) | |
(X-M)/(D-X) |
X = (1 - P)M + D × P
X = M ∙ PM + DP
(X - M) = P(D - M)
⇒ P = (X - M) / (D - M)
Question 16 |
Consider a long-lived TCP session with an end-to-end bandwidth of 1 Gbps (= 109 bits/second). The session starts with a sequence number of 1234. The minimum time (in seconds, rounded to the closest integer) before this sequence number can be used again is _________.
33 | |
34 | |
35 | |
36 |
The process of using all the sequence number and repeating a previously used sequence number.
The time taken to wrap around is called wrap around time:
Minimum Time = Wrap around time = Total number of bits in sequence number / Bandwidth = 232 * 8 / 109 = 34.35 == 34 (closest integer)
